Jörg Meyer, Hameln
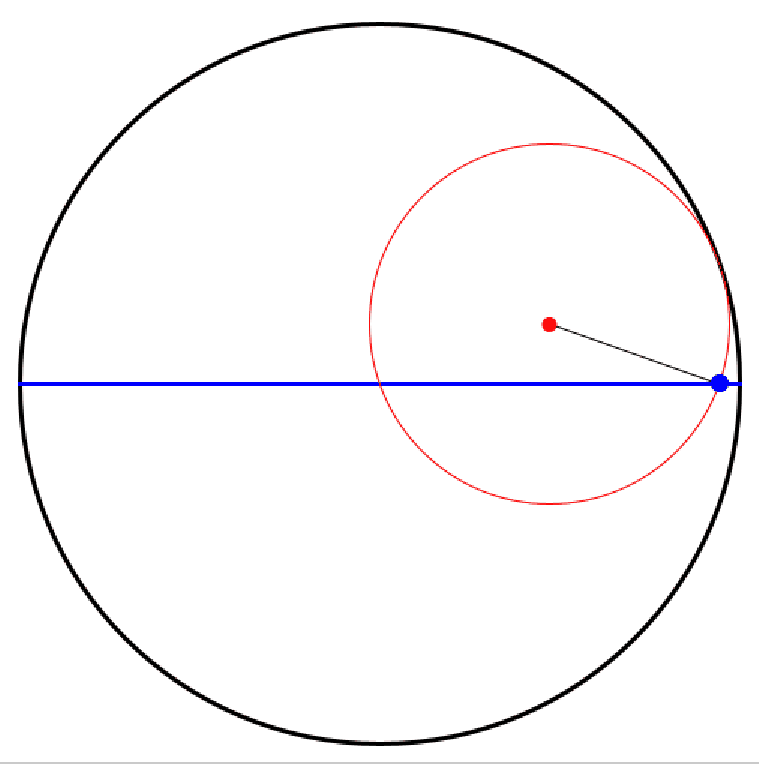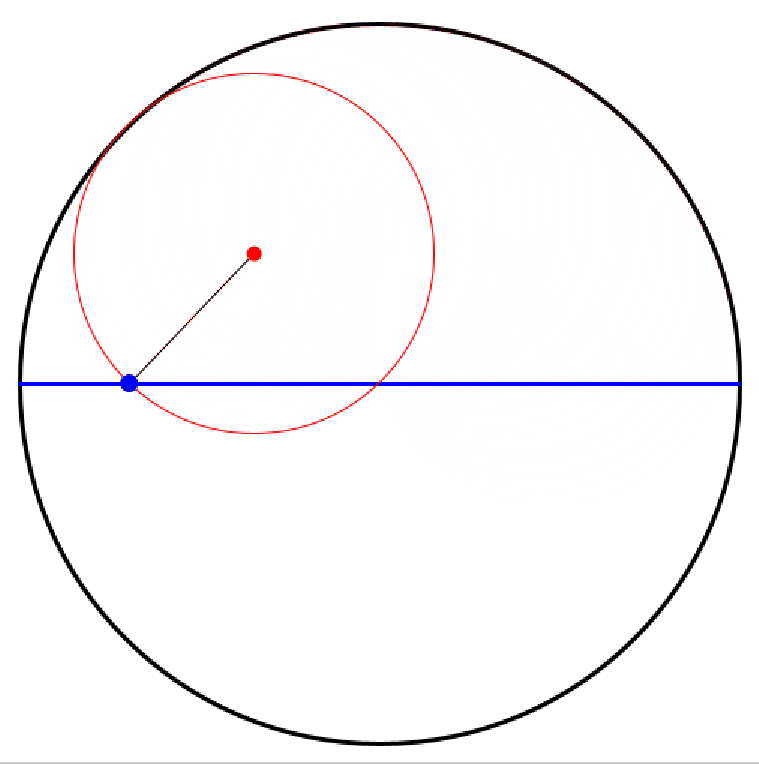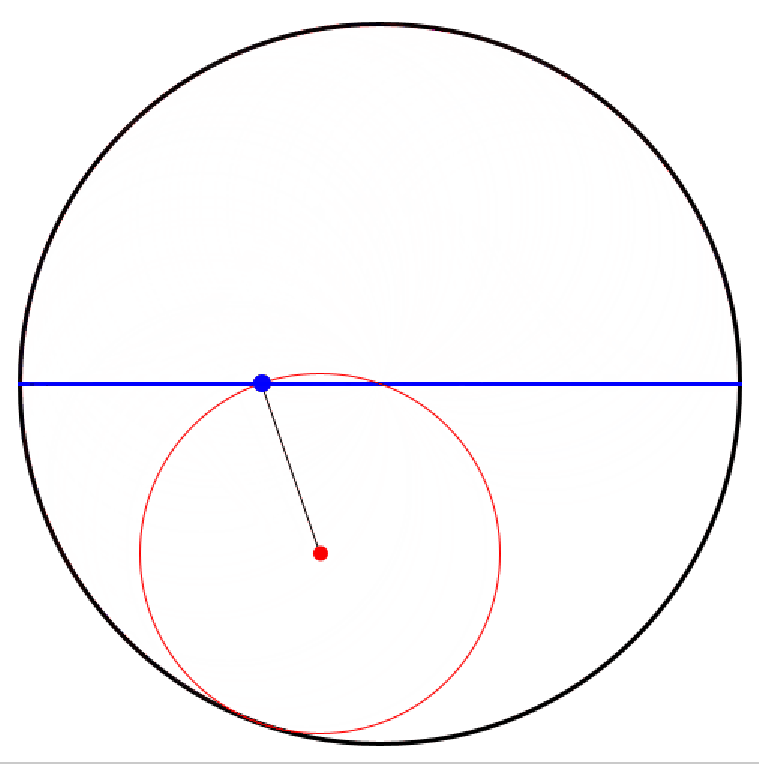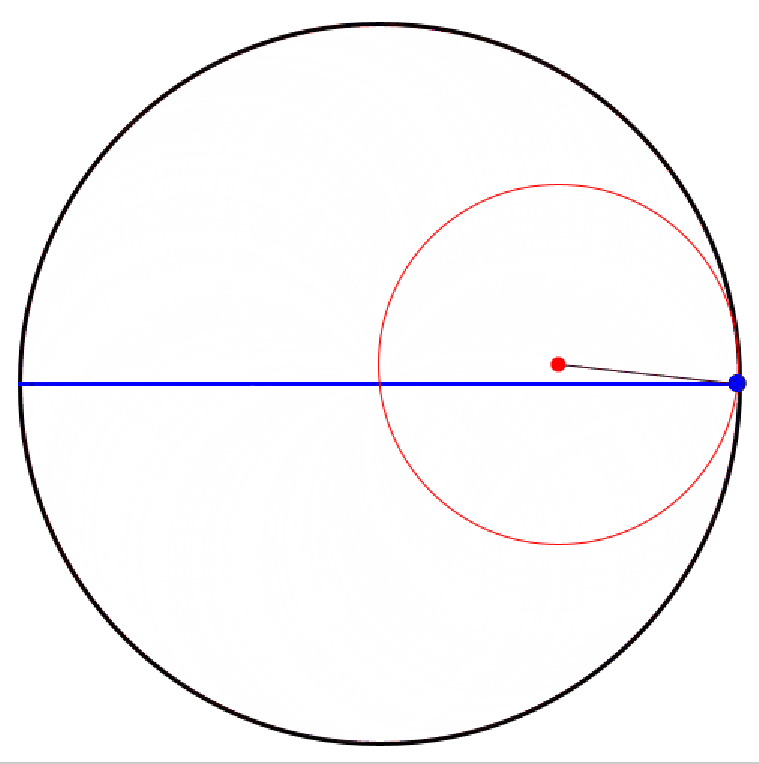
Rollt ein kleines (rotes) (Zahn-)Rad innen auf einem großen (schwarzen) (Zahn-)Rad ab, so beschreibt ein fester (blauer) Punkt auf dem kleinen (Zahn-)Rad eine Hypozykloide.
Ist der Radius des großen Rades genau doppelt so groß wie der Radius des kleinen Rades, so entartet die Hypozykloide zu einer (blauen) Strecke.
Damit gelingt die Transformation einer Kreisbewegung in eine geradlinige.
Ein fester (grüner) Punkt auf der Achse zwischen (blauem) Kurvenpunkt und (rotem)
Zentrum des kleinen Kreises beschreibt eine Ellipse, hier
die Begründung.
.
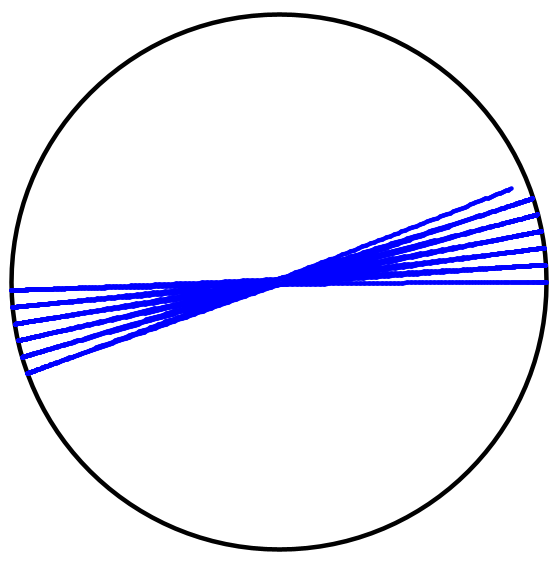
Die Zahnräder müssen für die Geradführung sehr genau gearbeitet sein.
Schon 1 Prozent Abweichung vom Verhältnis 2:1 führt zu starken Abweichungen,
die mit jeder Umdrehung größer werden.
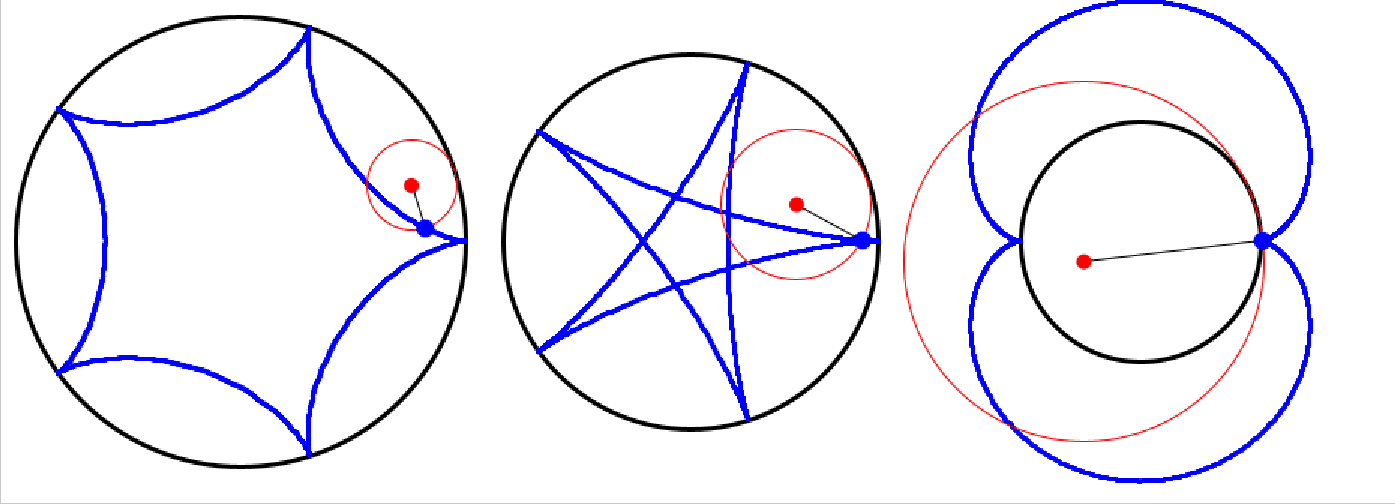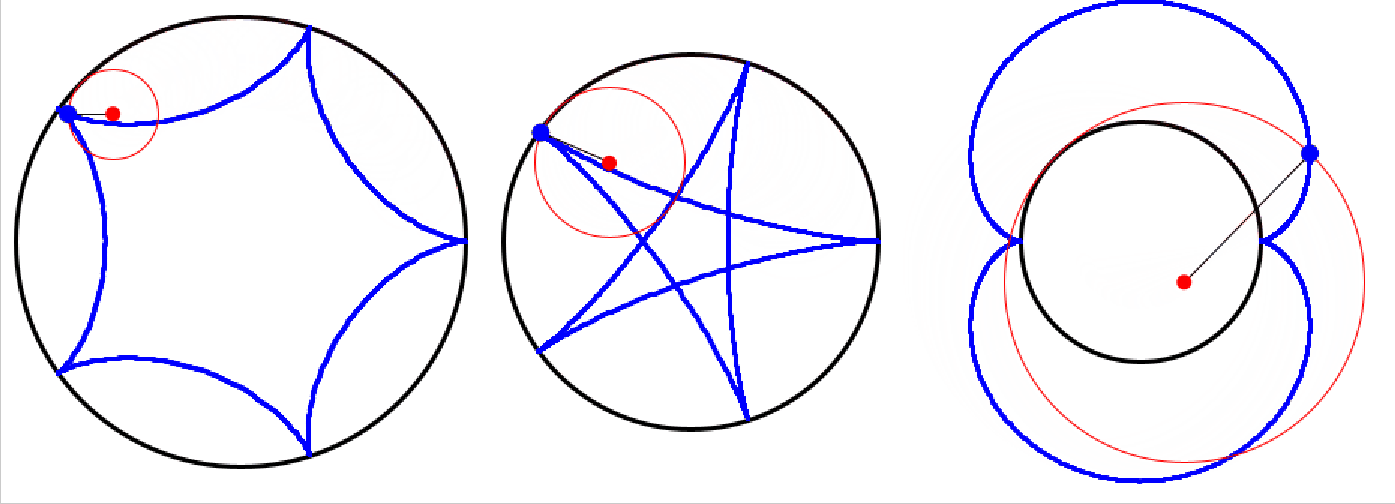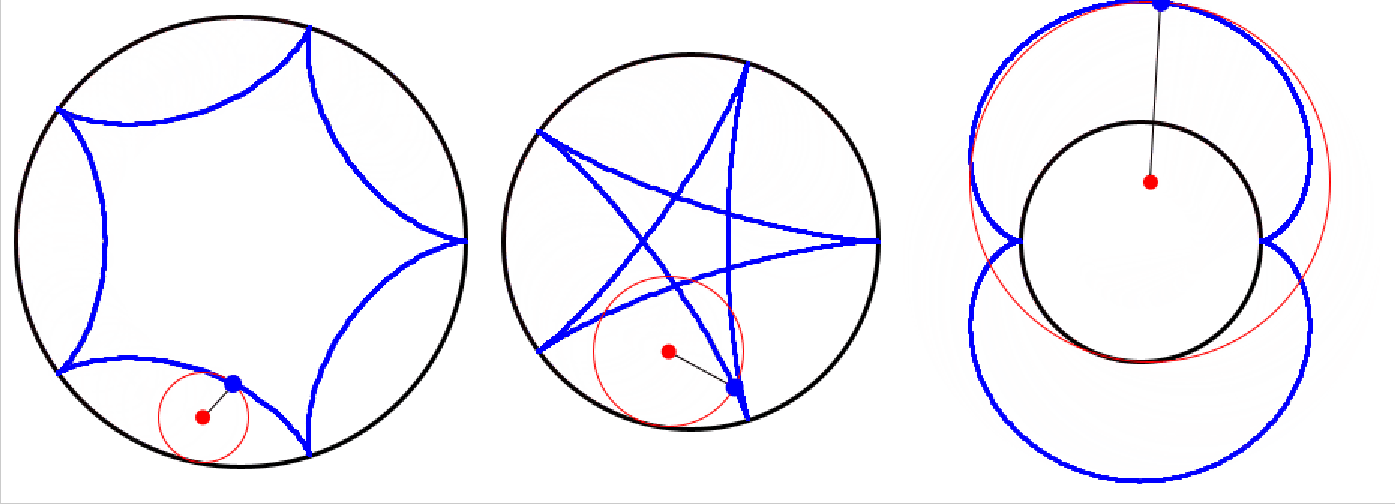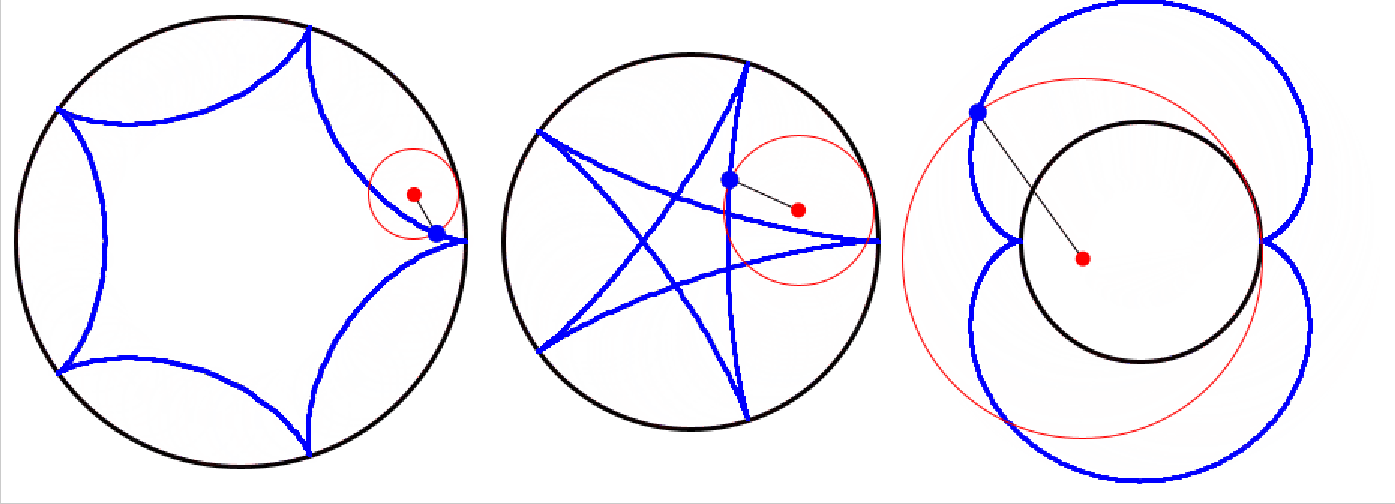
Links hat man R:r=5:1, in der Mitte 5:2 und rechts 2:3.
Es kann also auch ein größerer Kreis auf einem kleineren Kreis abrollen.