Jörg Meyer, Hameln

Wege zur Kopunktalität besonderer Dreieckslinien

Mittelsenkrechte

Natürlich könnte man starten mit der Aufforderung, dass alle ein Dreieck zeichnen sollen mit den drei Mittelsenkrechten. Mit hoher Wahrscheinlichkeit wird den Schülerinnen und Schülern gar nichts auffallen. Und selbst wenn jemand das Faktum, dass sich alle Mittelsenkrechten in nur einem einzigen Punkt schneiden, für bemerkenswert halten sollte, so zeigt doch die beliebige Variierbarkeit der Ausgangsdreiecks mit Geometrie-Software, dass der angesprochene Sachverhalt wohl allgemein gilt. Man hätte als Lehrperson eine viel bessere Ausgangsposition, wenn den Lernenden irgendetwas bei den Mittelsenkrechten als überraschend erscheinen würde, so dass ein Anlass zum Reden besteht. Dass die drei Mittelsenkrechten durch einen Punkt gehen, ist erfahrungsgemäß nicht überraschend.

Mit Hilfe von Geometrie-Software kann man aber folgendermaßen vorgehen: Man konstruiere ein Dreieck ABC und zwei Mittelsenkrechten, etwa m_a und m_b. Dass diese beiden Mittelsenkrechten sich schneiden, ist klar, da sie nicht zueinander parallel sein können. Der Schnittpunkt sei M. Nun kommt das Entscheidende: Man bewegt C mit der Maus und beobachtet, wie sich der Punkt M verhält. Dies Verhalten ist in der Tat überraschend: Obwohl C zweidimensional bewegt wird, bewegt sich M nur eindimensional! Wie kann man sich so etwas erklären?

Nun ist man – mit deutlich größerem Schülerinteresse – im Zentrum des klassischen Beweises: Was wissen wir über M?
M liegt auf m_b, also hat M denselben Abstand zu A und zu C.
M liegt auch auf m_a, also hat M denselben Abstand zu B und zu C.
Dann hat M auch denselben Abstand zu A und zu B. Daher liegt M auf der Mittelsenkrechten m_c. Anders formuliert: Also geht auch m_c durch M.

Innen-Winkelhalbierende

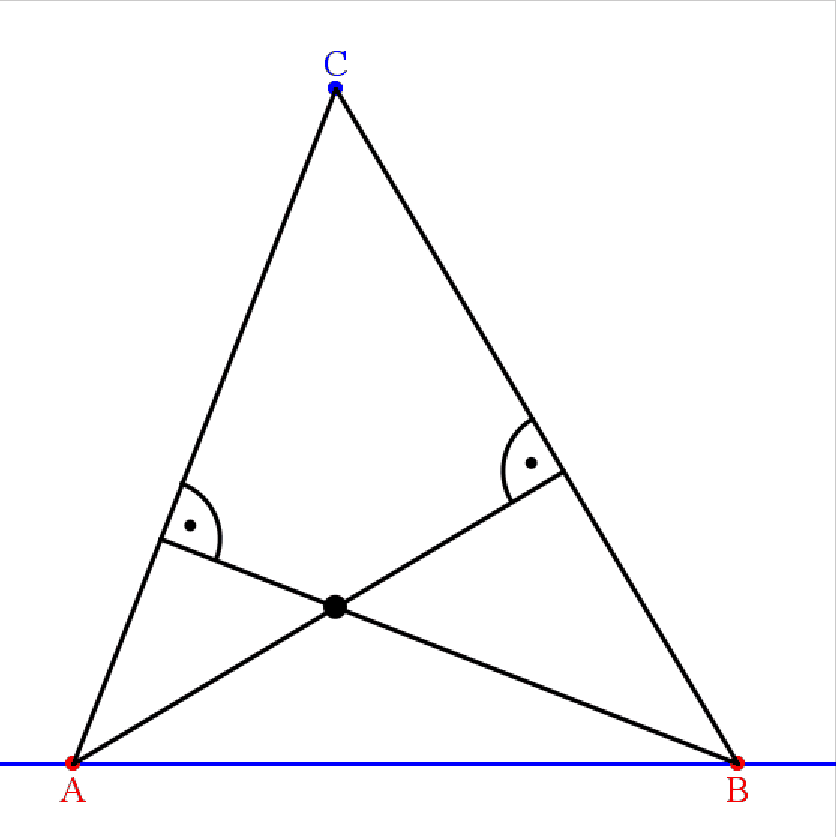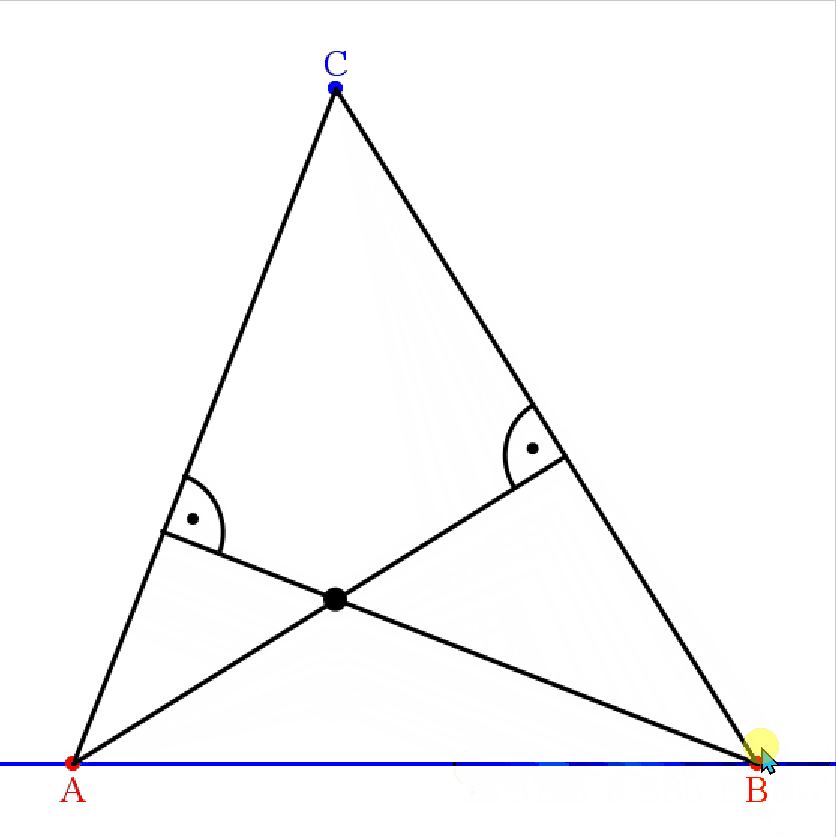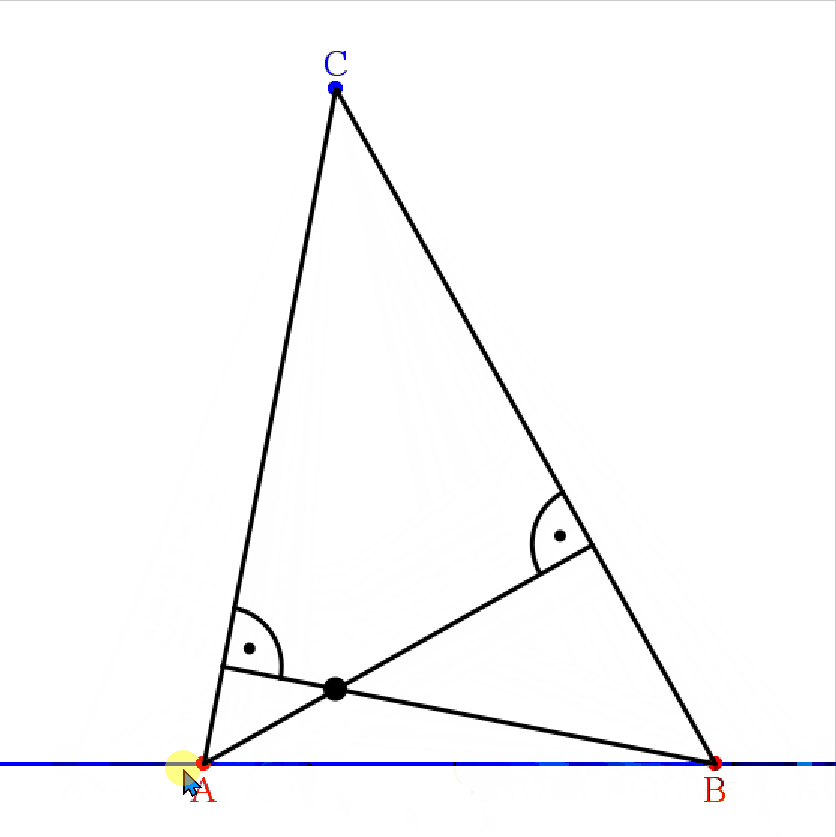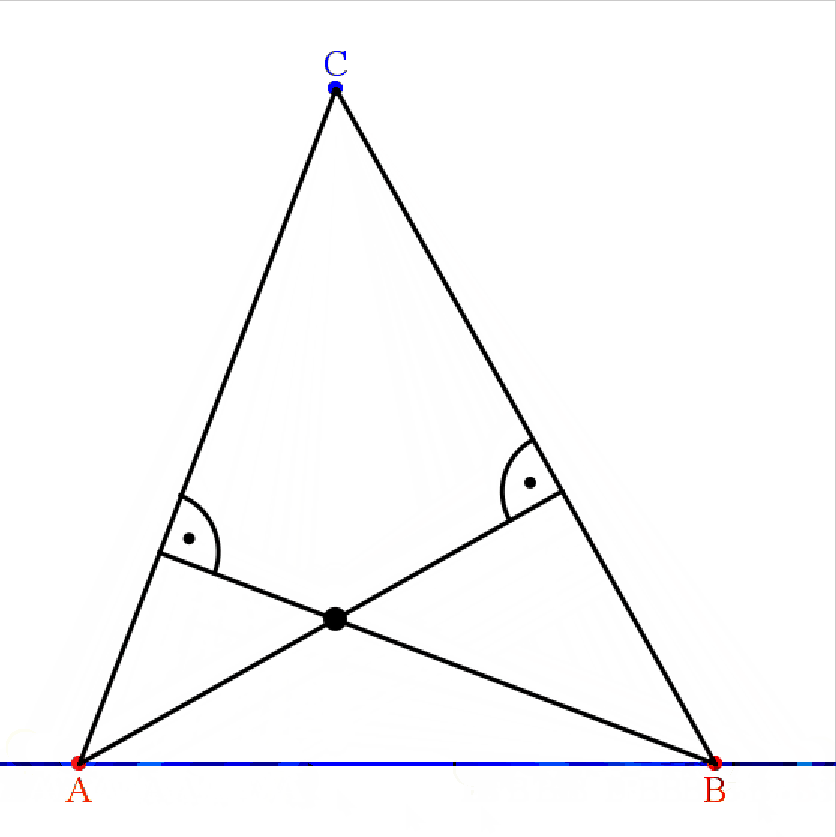
Eine Übertragung dieser Vorgehensweise auf Innen-winkelhalbierende liegt auf der Hand:
Man konstruiere die beiden Schenkel des Winkels γ und darauf A und B.
Die Winkelhalbierenden zu α und zu β schneiden sich in W. Bewegt man A oder B auf den jeweiligen Schenkeln, so beschreibt W offenbar eine Gerade. Warum ist das so?

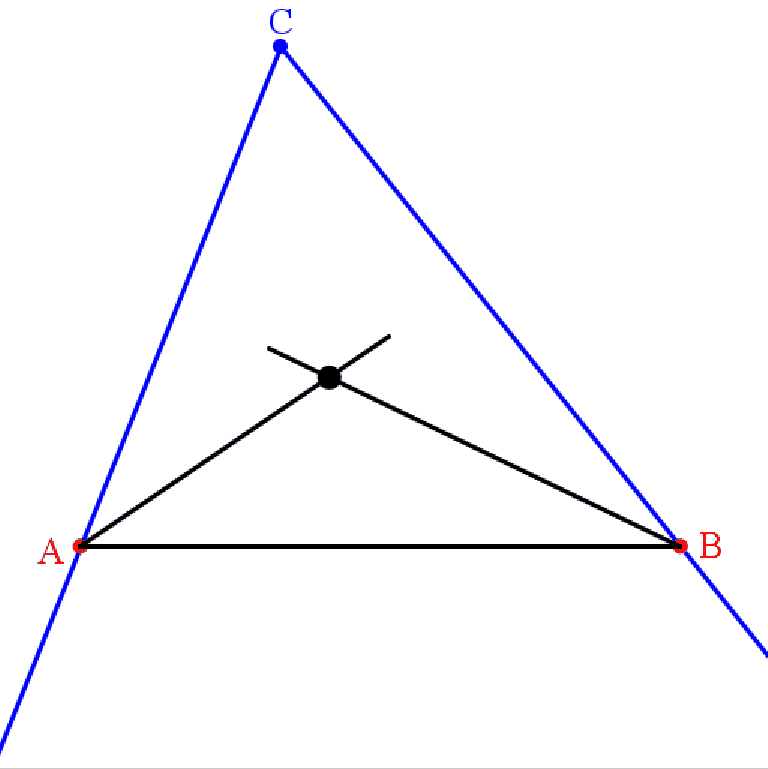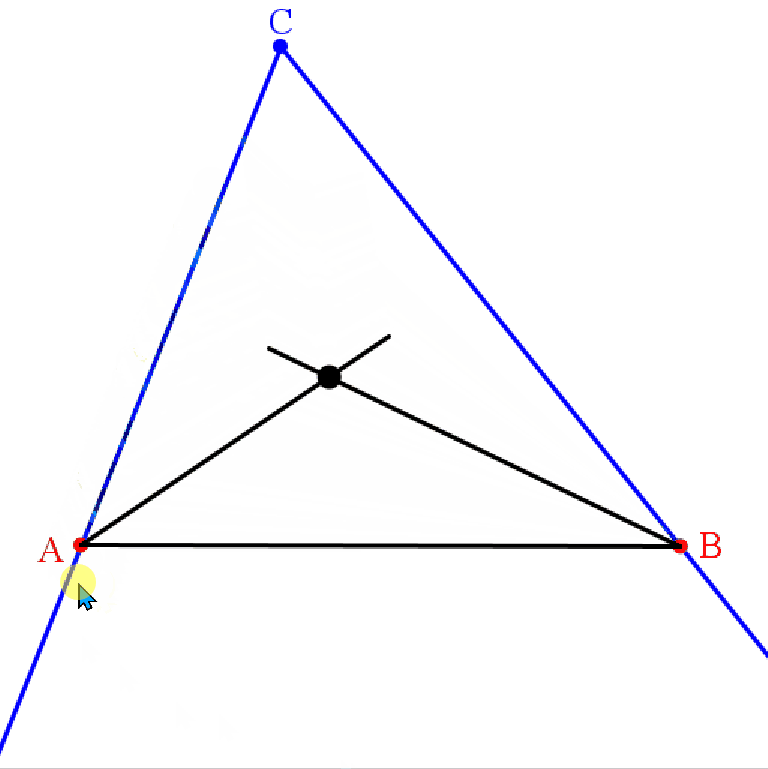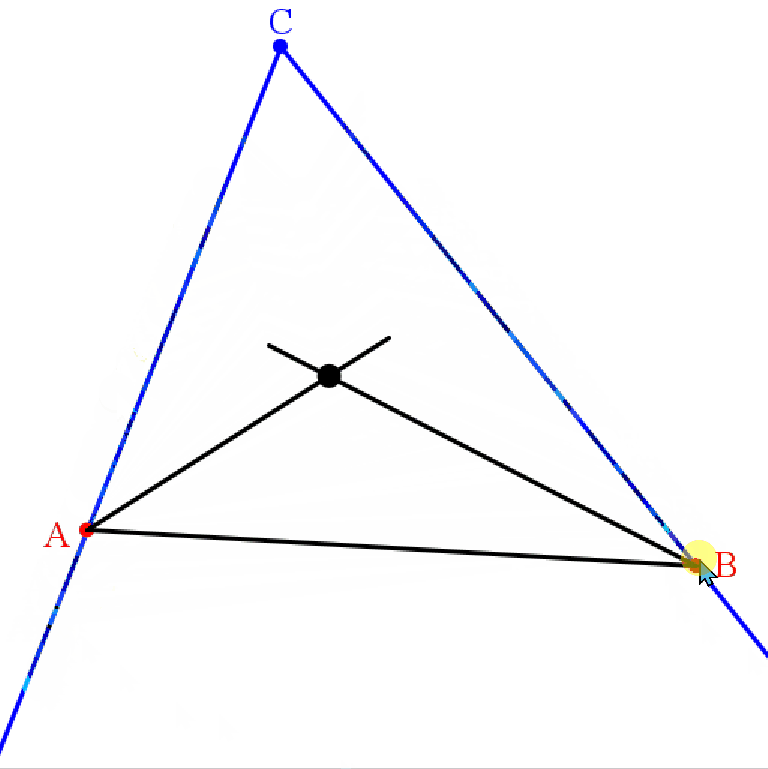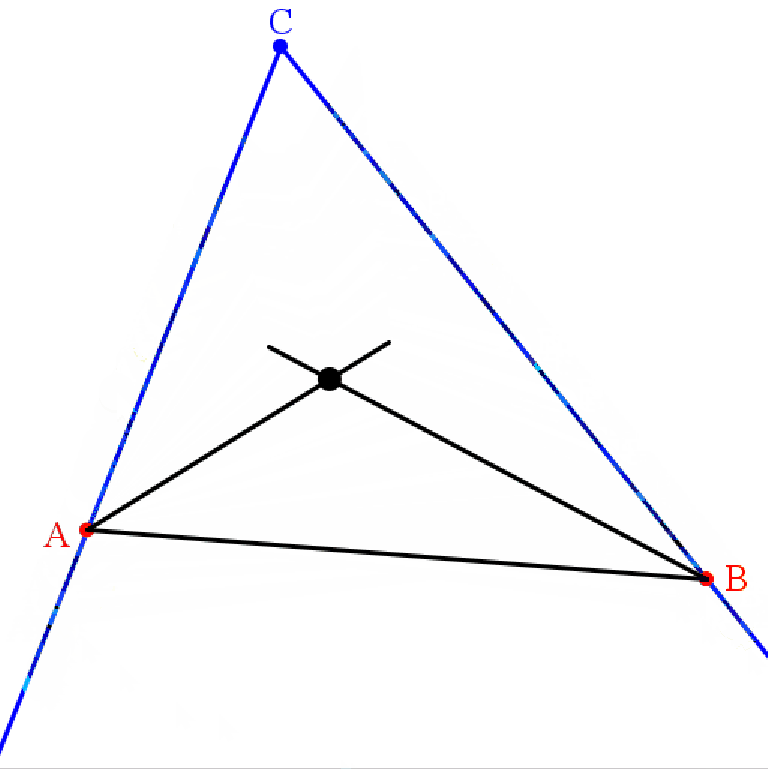
Was wissen wir über W?
W liegt auf w_α, also hat W denselben Abstand zu b und zu c.
W liegt auch auf w_β, also hat W denselben Abstand zu a und zu c.
Dann hat W auch denselben Abstand zu a und zu b. Daher liegt W auf der Winkelhalbierenden w_γ. Anders formuliert: Also geht auch w_γ durch W.

Diese Argumentation lässt sich auf Außen-Winkelhalbierende übertragen.

Seitenhalbierende

Man beginne mit C und M_c, dem Mittelpunkt der Seite c. Ein beliebiger Punkt A wird an M_c gespiegelt, um B zu erhalten. Die Seitenhalbierenden s_a und s_b schneiden sich in S. Bewegt man nun A zweidimensional, so ändert sich S überhaupt nicht. Wie ist das zu erklären?

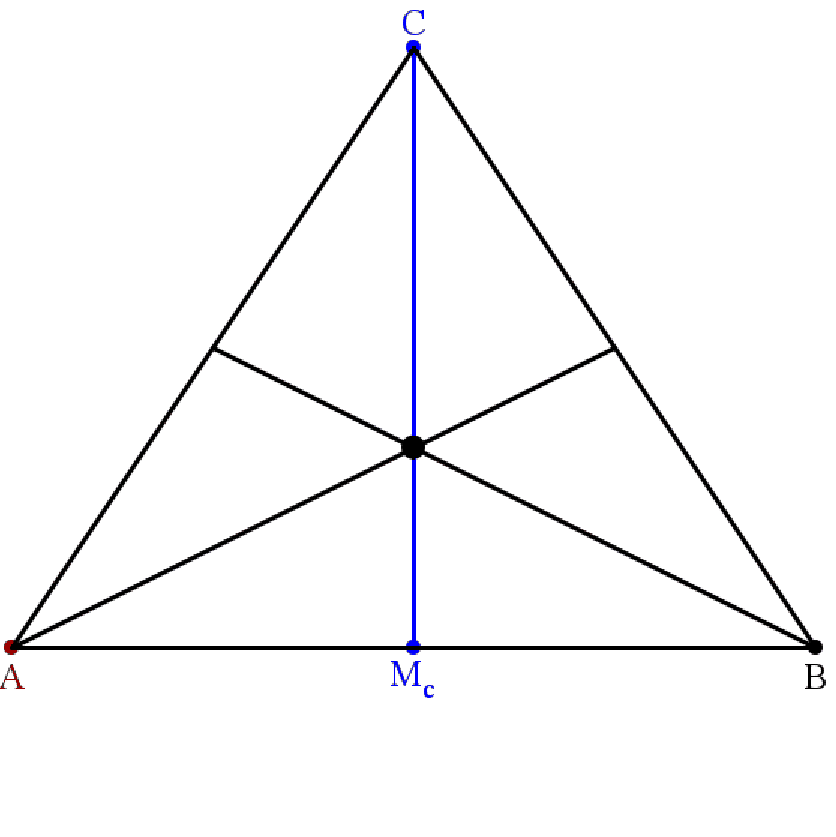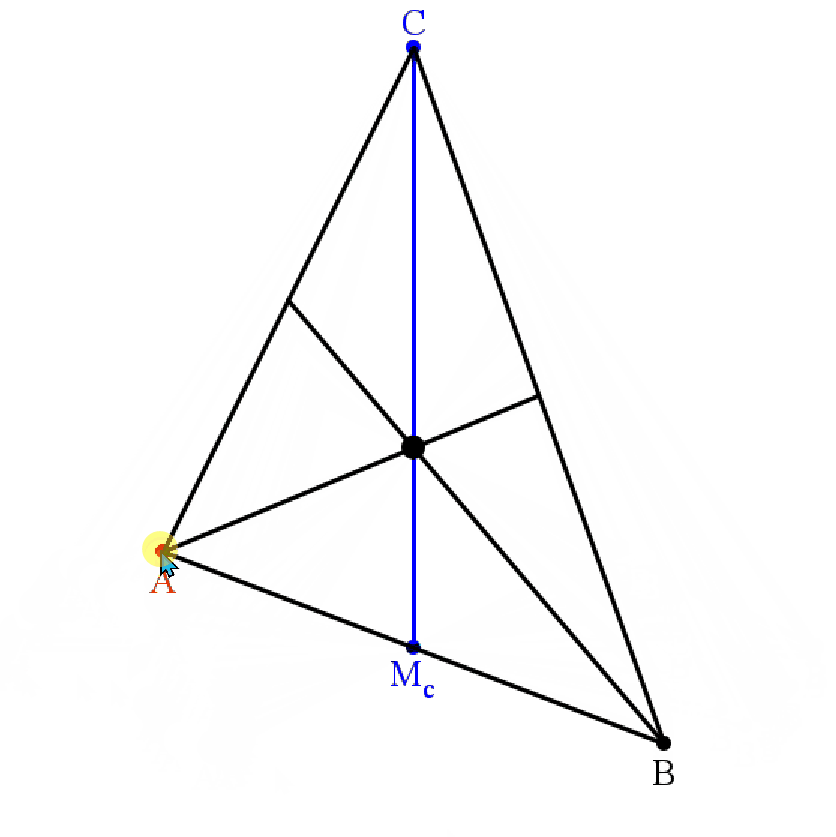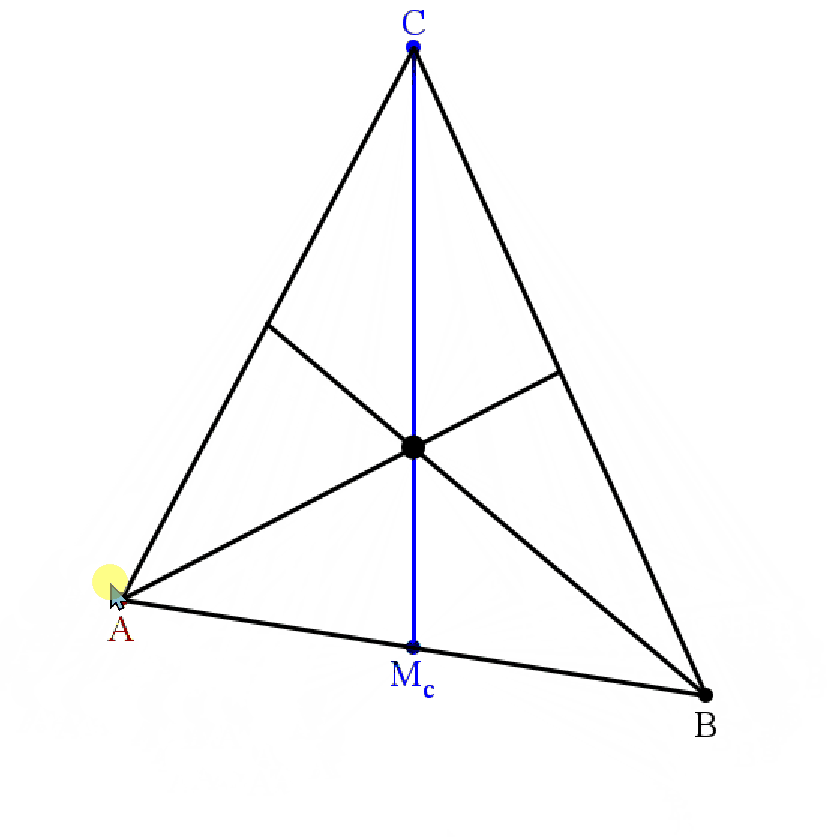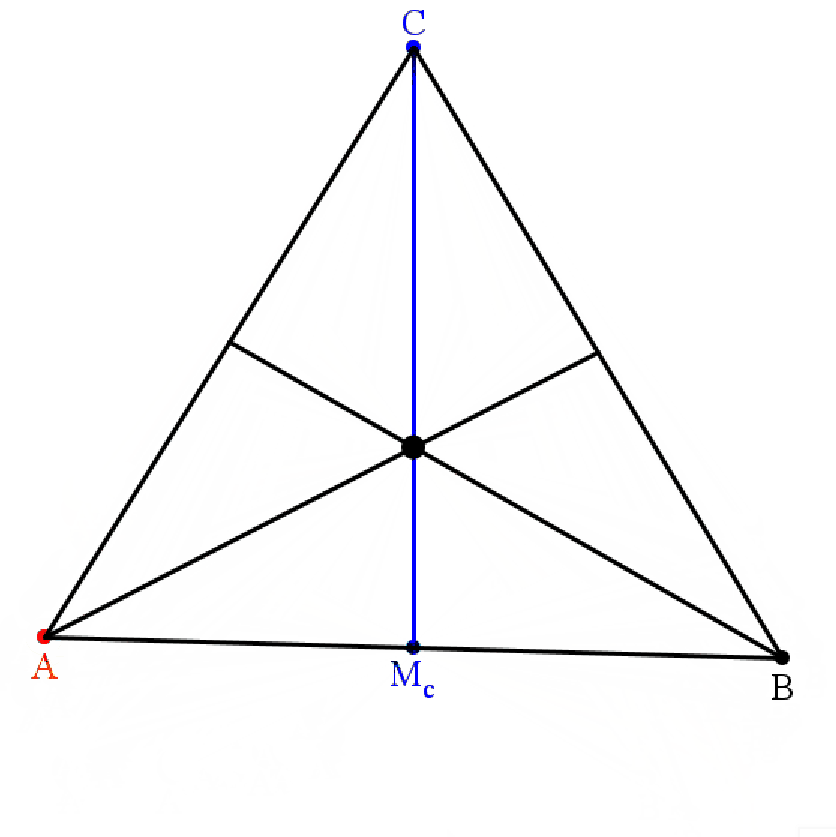
Dazu muss man die Seitenhalbierenden als Ortslinie interpretieren:

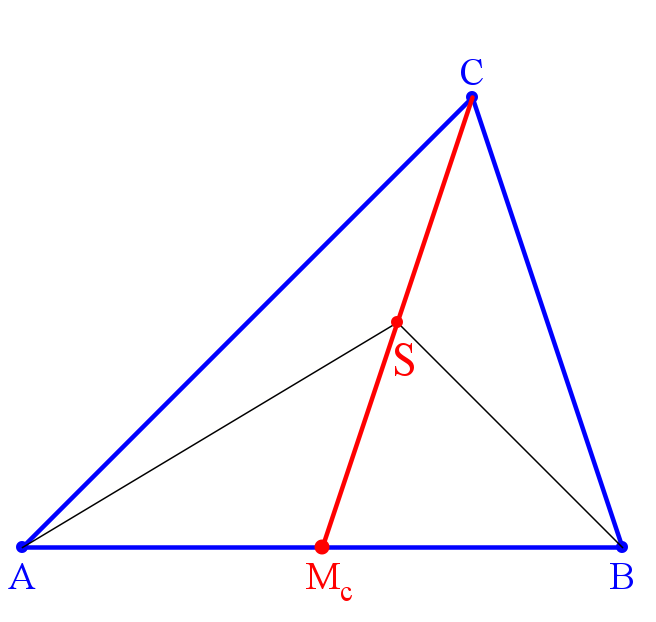
Bezeichnet man mit Fl den Flächeninhalt, so gilt einerseits Fl(AM_cC) = Fl(M_cBC).

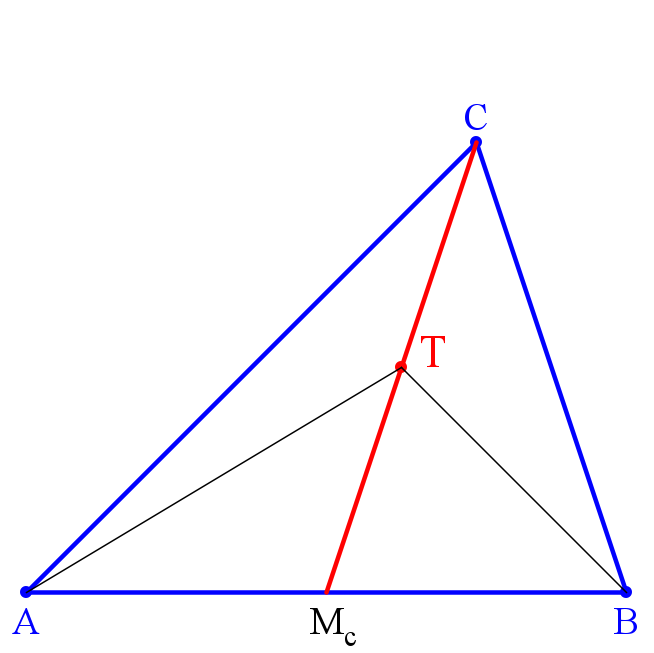
Genau für die Punkte T auf der Seitenhalbierenden s_c gilt außerdem Fl(AM_cT) = Fl(M_cBT).
Genau für die Punkte T auf der Seitenhalbierenden s_c gilt daher Fl(ATC) = Fl(TBC).

Damit ist die Charakterisierung der Punkte auf Seitenhalbierenden gefunden.

Nun sei S der Schnittpunkt der Seitenhalbierenden s_a und s_b.
S liegt auf s_a, also ist Fl(ASC) = Fl(ABS).
S liegt auf s_b, also ist Fl(ABS) = Fl(SBC).
Daher ist Fl(ASC) = Fl(SBC). Also liegt S auch auf s_c.

Höhen

Die Vorgehensweise lässt sich auch auf Höhen übertragen:
Man gehe aus vom Punkt C und einer beliebigen Geraden g, auf der C nicht liegt. Auf g wähle man zwei Punkte A und B und bilde daraus das Dreieck ABC. Die beiden Höhen h_a und h_b schneiden sich in H. Bewegt man A und B auf g, so beschreibt H eine Gerade. Warum? Was ist das für eine Gerade?